リストを扱う
池渕未来
作成 2011/05/10
章題の通り、3 章ではリストを扱います。これで少し「プログラムの性質の証明」らしくなっていますね。具体的にはリストの結合関数(app)、リバース関数(rev) を定義してその性質について証明してみます。これによってその性質に関して「絶対にバグのない」結合関数とリバース関数が書けることになります。わくわくして来ませんか?
リストの定義
2章でもちらっと出てきましたが、リストは以下のように定義されます。
Inductive list (A : Type) : Type := | nil : list A | cons : A -> list A -> list A.
list も前回の and や or のように、標準で定義されていてさらに最初からインポートされているので、自分で定義する必要はありません。
まずは、二つのリストの結合、app を定義してみます。app はこのように定義できます。
Fixpoint app (A : Type)(l l' : list A) : list A := match l with | nil => l' | cons x xs => cons x (app A xs l') end.
これまで関数の定義には Definition コマンドを使っていましたが、Definition そのものでは関数の再帰的定義ができません。再帰関数を定義するには、Fixpoint を使います。使い方はほとんど Definition と同じで、"Fixpoint" の後に関数名、引数、": 型"、":= 定義 ."、と書きます。
Fixpoint の他に、"match ~ with ~ end" といった新しい構文が見られますね。この match は、パターンマッチをしています。Coq では
match パターンマッチさせたい対象 with | パターン1 => 結果1 | パターン2 => 結果2 | ... end
と書くことによってパターンマッチができます。match の意味が理解できれば、なぜリストの結合があの app のような定義になるのかは分かるでしょう。
app も標準ライブラリで定義されており(定義は少し違いますが、挙動は同じです)、自分で定義しなくても使えます。また、標準ライブラリにある app は第一引数の A を渡さなくても暗黙に推論してくれるので "app l1 l2"と書きます。さらに list_scope というスコープの中では "cons x xs" を "x :: xs"、"app l1 l2" を "l1 ++ l2" の形で書けます。参考までに、app の定義を、定義の中で A を省略し cons を ::、app を ++ の形で置き変えた疑似コードを書いてみると以下のようになります。
(* 疑似コード *) Fixpoint ++ (l l' : list A) : list A := match l with | nil => l' | x :: xs => x :: (xs ++ l') end.
list_scope に入るには、
Open Scope list_scope.
とプログラムに記述し、list_scope を出るには
Close Scope list_scope.
と記述します。一般に "Open Scope (スコープ)." と "Close Scope (スコープ)." の間にあるプログラムは (スコープ) に入っています。
他にも標準ライブラリにある List モジュールをインポートすることによっても list_scope に入れます。List モジュールをインポートするには
Require Import List.
と書きます。List モジュールでは app の他に沢山の便利なリストに関する関数や定理が含まれています。
今回は後でこの Require Import を使います。
前置きが長くなりましたが、リストの性質を何か証明してみましょう。まず今定義した app の性質について示したいところですが、リストの証明には「リストの構造に関する帰納法」が重要になってくるので、先にその解説をします。
リストの構造に関する帰納法
数学的帰納法、という言葉は高校数学で習ったかと思います。ここでは「高校で習ったけどよく分からなかった」という方のためにリストの構造に関する帰納法について解説します。
一般に、リストに関して「帰納法による証明」とは以下のような定理を使って何らかの命題 P を証明することを言います。
型 A のリストに関する述語 P : list A -> Prop について、以下のことが成り立てば全てのリスト l について P(l) が成り立つ。
(1) P(nil) が成り立つ。
(2) 全ての値 x とリスト xs について、P(xs) が成り立てば P(x :: xs) も成り立つ。
この定理は「帰納法の原理」と呼ばれたりします。
全てのリストに関する命題の証明をしたいとき、リストはパターンが無限個あるので場合分け(case, destruct タクティク)だけでは証明は不可能なことが多いですが、帰納法(後述の induction タクティク)を使えば (1) と (2) だけ示せれば良いです。もちろん、帰納法を使わなくても証明できる命題や、帰納法を使っても証明できない命題もあります。
これだけ聞いてもよく分からないと思うので、たとえばこんな定理を証明したいとします。
app_nil_r : forall (A : Type)(l : list A), l ++ nil = l
"l ++ nil = l" は「l ++ nil と l が等しい」という命題を表わします。Coq の "a = b" は変数に a と b を取った型であり、Haskell や OCaml の "a == b" のようにブール値を返す訳ではありません。Haskell や OCaml の "==" は関数なのに Coq の "=" は型、ということに違和感を覚える方も多いかもしれませんが、「命題 <=> 型」という対応を思い出せば「a と b は等しい」は命題であるから "=" が型として表される、と理解できるでしょう。
app_nil_r の説明に戻ります。これは「すべてのリスト l は l ++ nil に等しい」という定理です。nil ++ l は app(++) の定義からそのまま l に等しいことが分かりますが、l ++ nil はすぐには分かりません。
では app_nil_r をまずは proof-editing mode ではなく言葉の上で帰納法を使って証明してみます。
(1) nil ++ nil = nil は ++ の定義から明らか。
(2) リスト xs に対して xs ++ nil = xs を仮定する。任意の値 x に対し、(x :: xs) ++ nil = x :: xs を示す。
(x :: xs) ++ nil = x :: (xs ++ nil) (++ の定義より)
= x :: xs (帰納法の仮定より)
(1)(2) より全てのリスト l に対して l ++ nil = l が示せた。
次の小節からは proof-editing mode を使って帰納法による証明をしてみましょう。
app_nil_r の証明
app_nil_r を proof-editing mode を使って証明してみます。
Require Import List. Theorem app_nil_r : forall (A : Type)(l : list A), l ++ nil = l.
intros をしてみるとサブゴールが以下のように変わります。
intros.
1 subgoal A : Type l : list A ______________________________________(1/1) l ++ nil = l
この次はリスト l に関する帰納法で証明を進めてみようと思います。詳しく言うと、
全てのリスト l に対して "l ++ nil = l" が成り立つ
ということを
(1) nil ++ nil = nil (2) l ++ nil = l ⇒ (a :: l) ++ nil = a :: l
の二段階に分けて示します。a は Coq が自動で選んだ変数名です。帰納法で証明を進めるには induction というタクティクを使います。
induction l.
2 subgoals A : Type ______________________________________(1/2) nil ++ nil = nil ______________________________________(2/2) (a :: l) ++ nil = a :: l
一つ目のサブゴールは帰納法の (1) に対応していることが分かります。二つ目はサブゴールだけ表示されていて仮定は表示されていませんが、Command Pane に
(左のテキストボックス)Show (右のテキストボックス)2
と打って Ok を選択すれば
Result for command Show 2 . : subgoal 2 is: A : Type a : A l : list A IHl : l ++ nil = l ============================ (a :: l) ++ nil = a :: l
のように二つ目の仮定とサブゴールが表示されます。帰納法の (2) は "P(xs) が成り立てば P(x::xs) も成り立つ" でしたが、IHl1 が P(xs)、サブゴールは P(x::xs) に対応していることが分かりますね。
"induction x." は現在の証明図を見て、今何を示したいのかを調べます。この例では今示したいことは単にサブゴールそのままです。そして x について帰納法で証明するように仮定とサブゴールを書き換えます。リストに関する帰納法なので (1) と (2) の二段階に分けて示します。x はリストである必要はなく、Inductive を使って定義されたデータ型に対して使えます。 "induction l." で l についての帰納法が使えます。一つ目のサブゴールが帰納法の (1) に、二つ目のサブゴールが (2) に対応するようになります。
証明に戻ります。"nil ++ nil" は ++ の定義から nil に簡約され、左辺と右辺は等しくなります。これを示すには、reflexivity タクティクを使います。reflexivity タクティクは、サブゴールが等式の形のとき、左辺と右辺の値が等しい場合に使えます。
reflexivity.
1 subgoal A : Type a : A l : list A IHl : l ++ nil = l ______________________________________(1/1) (a :: l) ++ nil = a :: l
この次も "(a :: l) ++ nil" は ++ の定義から "a :: (l ++ nil)" に簡約できます。定義から明らかに簡約できる式を簡約するには、simpl タクティクを使います。
simpl.
1 subgoal A : Type a : A l : list A IHl : l ++ nil = l ______________________________________(1/1) a :: l ++ nil = a :: l
++ は :: より優先順位が高いので、"a :: l ++ nil" は "a :: (l ++ nil)" となります。仮定を見ると IHl という名前で "l ++ nil = l" が分かっているので、両辺に cons a を適用すればこのサブゴールは正しいことが分かります。このことを Coq に伝えるには、f_equal という定理を使います。f_equal の型は
f_equal : forall (A B : Type) (f : A -> B) (x y : A), x = y -> f x = f y
です。これは "x = y" ならばどんな関数 f に対しても "f x = f y" だということを言っています。今回は f は "cons a"、つまり "fun xs => a :: xs" ですね。
Command Pane で "Print f_equal" と打って関数定義を表示させると下から二番目の行に
Arguments A, B, x, y are implicit
とありますが、これは A B x y はそれぞれ f_equal に渡さず省略できるという意味です。では f_equal に (cons a) を渡して apply しましょう。
apply (f_equal (cons a)).
1 subgoal A : Type a : A l : list A IHl : l ++ nil = l ______________________________________(1/1) l ++ nil = l
サブゴールが IHl の型そのものになったので、apply すれば証明終了です。
apply IHl.
Proof completed.
今回の証明で "apply (f_equal X)." を使いましたが、もっと短く f_equal というタクティクを使っても同じ動作をします。
f_equal.
"apply (f_equal X)." のときと違って X を与えていませんが、Coq が推論してくれます。便利なのでどんどん使いましょう。
app の性質の証明
以下のような app_assoc を proof-editing mode で証明してみます。
Require Import List. Theorem app_assoc : forall (A : Type)(l1 l2 l3 : list A), l1 ++ (l2 ++ l3) = (l1 ++ l2) ++ l3.
山本先生からの一言
ここはリストの結合律のお話です。Haskell で書くと以下のようになります。
xs ++ (ys ++ zs) = (xs ++ ys) ++ zs
この等式が成り立つことは直感的には明らかですが、どのように証明されるのでしょうか。まずは intros をしてみます。
intros.
1 subgoal A : Type l1 : list A l2 : list A l3 : list A ______________________________________(1/1) l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3
++ は右結合的なので "l1 ++ l2 ++ l3" は "l1 ++ (l2 ++ l3)" となります。今回は l1 に関する帰納法で証明を進めようと思います。
induction l1.
2 subgoals A : Type l2 : list A l3 : list A ______________________________________(1/2) nil ++ l2 ++ l3 = (nil ++ l2) ++ l3 ______________________________________(2/2) (a :: l1) ++ l2 ++ l3 = ((a :: l1) ++ l2) ++ l3
一つ目のサブゴールは両辺のどちらも簡約すると l2 ++ l3 になるので、reflexivity タクティクが使えます。
reflexivity.
1 subgoal A : Type a : A l1 : list A l2 : list A l3 : list A IHl1 : l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3 ______________________________________(1/1) (a :: l1) ++ l2 ++ l3 = ((a :: l1) ++ l2) ++ l3
サブゴールが残り一つになりました。今度のサブゴールは "(a :: l1) ++ X" の形があり、これも定義から "a :: (l1 ++ X)" に簡約できますね。もう一度 simpl タクティクを使いましょう。
simpl.
1 subgoal A : Type a : A l1 : list A l2 : list A l3 : list A IHl1 : l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3 ______________________________________(1/1) a :: l1 ++ l2 ++ l3 = a :: (l1 ++ l2) ++ l3
app_nil_r のときと同じく両辺に "a ::" がかかっているので、f_equal タクティクが使えます。
f_equal.
1 subgoal A : Type a : A l1 : list A l2 : list A l3 : list A IHl1 : l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3 ______________________________________(1/1) l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3
このサブゴールは IHl1 の型そのままですね。apply すれば証明終了です。
apply IHl1. Qed.
app_assoc is defined
これで、どんなリスト l1 l2 l3 に対しても "l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3" であることが保証されました。
少し長くなったので今回の証明をまとめて書きます。
Require Import List. Theorem app_assoc : forall (A : Type)(l1 l2 l3 : list A), l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3. intros. induction l1. (* 1 *) reflexivity. (* 2 *) simpl. f_equal. (* apply (f_equal (cons a)). でも OK *) apply IHl1. Qed.
rev の性質
app 以外の関数の性質を証明してみましょう。Coq の List モジュールではリストの要素を逆転させる関数、rev が用意されています。
Require Import List. Fixpoint rev (A : Type)(l : list A) : list A := match l with | nil => nil | x :: xs => rev xs ++ (x :: nil) end.
Command Pane で "Print rev" とすれば "Argument A is implicit" とあり、A は省略できることが分かります。
rev には、こんな性質が成り立ちます。
rev_app_distr : forall (A : Type)(l1 l2 : list A), rev (l1 ++ l2) = rev l2 ++ rev l1
具体的に l1 や l2 に何か値を代入して考えれば直感的には自明でしょう。
山本先生からの一言
revの性質は、手を使って考えると分かり易いでしょう。下の図を見て下さい。右手と左手の全体をひっくり返した状態は、左右の手をそれぞれ反転し左右の入れ替えた状態と同じですね。
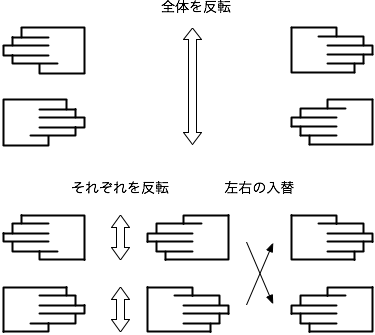
ではこれを証明してみようと思います。
Theorem rev_app_distr : forall (A : Type)(l1 l2 : list A), rev (l1 ++ l2) = rev l2 ++ rev l1.
まずはいつも通り intros をします。
intros.
1 subgoal A : Type l1 : list A l2 : list A ______________________________________(1/1) rev (l1 ++ l2) = rev l2 ++ rev l1
app のときと同じように、また l1 について帰納法を使ってみます。
induction l1.
2 subgoals A : Type l2 : list A ______________________________________(1/2) rev (nil ++ l2) = rev l2 ++ rev nil ______________________________________(2/2) rev ((a :: l1) ++ l2) = rev l2 ++ rev (a :: l1)
このサブゴールは簡約できますね。simpl タクティクの出番です。
simpl.
2 subgoals A : Type l2 : list A ______________________________________(1/2) rev l2 = rev l2 ++ nil ...
ここで、"rev l2 ++ nil" は帰納法の説明のときに示した app_nil_r の型ですね。app_nil_r は自分で定義しなくても List モジュールで既に定義されているので List モジュールをインポートしていれば使えます。
app_nil_r : forall (l : list A), l ++ nil = l
これをそのまま apply したいところですが、右辺と左辺が逆になってしまっています。ここで、rewrite というタクティクを紹介します。
rewrite app_nil_r.
2 subgoals A : Type l2 : list A ______________________________________(1/2) rev l2 = rev l2 ...
右辺の "rev l2 ++ nil" が、"rev l2" に書き変わりました。"rewrite X." は、X が "forall 〜, a = b" という型をしているとき、サブゴール中の a を b に書き換えます。逆に、b を a に書き換えたいときは "rewrite <- X." のようにします。
これで今度は reflexivity を適用できます。
reflexivity.
1 subgoal A : Type a : A l1 : list A l2 : list A IHl1 : rev (l1 ++ l2) = rev l2 ++ rev l1 ______________________________________(1/1) rev ((a :: l1) ++ l2) = rev l2 ++ rev (a :: l1)
サブゴールが一つになりました。このサブゴールもまた "(a :: l1) ++ l2" を "a :: l1 ++ l2" に、"rev (a :: l1)" を "rev l1 ++ (a :: nil)" に簡約できますね。
simpl.
1 subgoal A : Type a : A l1 : list A l2 : list A IHl1 : rev (l1 ++ l2) = rev l2 ++ rev l1 ______________________________________(1/1) rev (l1 ++ l2) ++ a :: nil = rev l2 ++ rev l1 ++ a :: nil
ここで、両辺の "++ a :: nil" を f_equal を使って取ればサブゴールが IHl1 の型そのままになりそうですが、++ は右結合的なので "rev l2 ++ rev l1 ++ a :: nil" は "rev l2 ++ (rev l1 ++ a :: nil)" となり、"++ a :: nil" を取ることができません。
そこで、前に証明した、app_assoc の出番です。app_assoc の型は
app_assoc : forall (A : Type)(l1 l2 l3 : list A), l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3
で、rewrite タクティクを使えば "rev l2 ++ rev l1 ++ a :: nil" を "(rev l2 ++ rev l1) ++ a :: nil" に書き換えられますね。
rewrite app_assoc.
1 subgoal A : Type a : A l1 : list A l2 : list A IHl1 : rev (l1 ++ l2) = rev l2 ++ rev l1 ______________________________________(1/1) rev (l1 ++ l2) ++ a :: nil = (rev l2 ++ rev l1) ++ a :: nil
これで f_equal を使って "++ a :: nil" を取れます。
f_equal.
1 subgoal A : Type a : A l1 : list A l2 : list A IHl1 : rev (l1 ++ l2) = rev l2 ++ rev l1 ______________________________________(1/1) rev (l1 ++ l2) = rev l2 ++ rev l1
サブゴールが IHl1 の型そのままになりました。apply すれば証明は終わりです。
apply IHl1. Qed.
証明のまとめを書きます。
Theorem rev_app_distr : forall (A : Type)(l1 l2 : list A), rev (l1 ++ l2) = rev l2 ++ rev l1. intros. induction l1. (* 1 *) simpl. rewrite app_nil_r. reflexivity. (* 2 *) simpl. rewrite app_assoc. f_equal. apply IHl1. Qed.
Fixpoint についての注意
Coq では、再帰関数は無限ループにならないこと、つまり停止性が保証されていないと処理系は受理してくれません。
再帰関数を定義するコマンドは Fixpoint と Function がありますが、Fixpoint で定義した関数はその引数のどれかが再帰的に呼び出すごとに構造が小くなっていく必要があります。
具体的にリストで言うと、app も rev も、x::xs を渡すと次の app、rev には xs を渡して、再帰呼び出しごとに app や rev の引数は小くなって最終的に nil になり停止しますね。
そのため Fixpoint で再帰関数を定義するときは、引数のどれかが小くなっていくように注意して定義してください。Function を使って定義するともっと柔軟に、停止性は頭で考えて分かるけれど Fixpoint で定義しづらい(もしくは、できない)関数も定義できるようになりますが、それは別の章で説明します。
タクティクまとめと帰納法を使った証明のテクニック
また新しいタクティクが登場したので、まとめておきます。
| induction x | x について帰納法で証明を進める |
| simpl | サブゴールを簡約する |
| reflexivity | サブゴールが等式の形で、両辺の値が等しいとき |
| f_equal | apply (f_equal x) のようなもの、x は省略できる |
| rewrite x | x の型が "forall 〜, a = b" のとき、サブゴールの a を b で書き換える |
| rewrite <- x | x の型が "forall 〜, a = b" のとき、サブゴールの b を a で書き換える |
app_assoc や rev_app_distr の証明はこちらが手順を全て教えましたが、タクティクの使い方が分かっても自分で証明するとなると難しいかと思います。「どうすれば証明の手順が思い付くのか」は簡単な問題ではありませんが、「こうすれば上手くいくことが多い」という王道のようなものはあるので、帰納法で証明するときのそれを紹介します。
app_assoc や rev_app_distr の証明では、どちらも intros した後に l1 についての帰納法(induction l1)で証明を進めました。なぜそこで帰納法を使って、しかも l1 についての帰納法なのかというと、そのときのサブゴールを見て判断しました。intros 後の app_assoc、rev_app_distr のサブゴールはこうでした。
l1 ++ l2 ++ l3 = (l1 ++ l2) ++ l3 (* app_assoc *) rev (l1 ++ l2) = rev l2 ++ rev l1 (* rev_app_distr *)
まず、このときとくに証明を進めるのに使えそうな仮定もなかったので、場合分け(destruct、case)か帰納法(induction)で証明することくらいが先に進む手段です(外にある定理を使うこともできますが、ここでは考えません)。ここで destruct を使うと、二つ目のサブゴールで結果的に帰納法の仮定(今回の IHl1)がないのでそれ以上証明が進まなくなってしまうため induction を使いました。結果論ですがこのことは慣れると予想できるようになりますが、最初はとりあえず destruct でやってみて行き詰まったら戻って induction に変えてみるか、最初から induction で進めてしまうのが良いでしょう。
次に induction で進めるべきと分かっても、どうして l2 や l3 でなく l1 について induction を使ったのかについて解説します。上の二つのサブゴールを見ると、関数 ++ があります。++ の疑似コードはこうでした。
(* 疑似コード *) Fixpoint ++ (l l' : list A) : list A := match l with | nil => l' | x :: xs => x :: (xs ++ l') end.
この定義を見ると、++ の第一引数が nil か x::xs の形をしていれば l ++ l' は簡約できることが分かります。一方 induction l を使うと、一つ目のサブゴールでは l は nil に、二つ目のサブゴールでは l は a::l になりましたね。よって、"X ++ Y" がサブゴールにあるとき、induction の対象が Y だと ++ はそれ以上簡約できませんが、X だと induction タクティクを使った後、それぞれのサブゴールで "nil ++ Y"、"a::X ++ Y" となり簡約でき、証明が進めやすくなるので、 app_assoc や rev_app_distr のときは l1 を induction の対象にしたのでした。
このように、他に証明を進める手段がなさそうだったら、サブゴールが簡約できるように induction や destruct を使うと上手く行くことが多いです。
これをふまえて、次の練習問題に取り組んでみてください。
練習問題
問6. リストを二回 rev したら元に戻るという定理、つまり
rev_involutive : forall (A : Type)(l : list A), rev (rev l) = l
を証明しなさい。
問7. List モジュールには以下のような関数 fold_right があります。
Fixpoint fold_right (A B : Type)(f : B -> A -> A)(a0 : A)(l : list B) : A := match l with | nil => a0 | b :: t => f b (fold_right A B f a0 t) end. (ただし標準ライブラリにある fold_right を使う場合は A B は省略可)
この関数についての以下の定理を証明しなさい。
fold_right_app : forall (A B : Type)(f : B -> A -> A)(l l' : list B)(i : A), fold_right f i (l ++ l') = fold_right f (fold_right f i l') l
前回の答え
前回の問題は、
問2. forall (P Q R : Prop), (P -> Q) -> (Q -> R) -> P -> R 問3. forall (P : Prop), ~(P /\ ~P) 問4. forall (P Q : Prop), ~P \/ ~Q -> ~(P /\ Q) 問5. forall (P : Prop), (forall (P : Prop), ~~P -> P) -> P \/ ~P
でした。それぞれを problem2、problem3、problem4、problem5 とします。答えは一通りではないので、下に書くのは一つの例です。
Theorem problem2 : forall (P Q R : Prop), (P -> Q) -> (Q -> R) -> P -> R. intros. apply H0. apply H. apply H1. Qed. Theorem problem3 : forall (P : Prop), ~(P /\ ~P). unfold not. intros. destruct H. apply (H0 H). Qed. Theorem problem4 : forall (P Q : Prop), ~P \/ ~Q -> ~(P /\ Q). unfold not. intros. destruct H0. destruct H. apply (H H0). apply (H H1). Qed. Theorem problem5 : forall (P : Prop), (forall (P : Prop), ~~P -> P) -> P \/ ~P. unfold not. intros. apply H. intros. apply H0. right. intros. apply H0. left. apply H1. Qed.


山本先生からの一言
ここはリストの左単位元と右単位元のお話です。Haskell で書くと以下のようになります。