証明駆動開発入門(1)

池渕未来
公開 2011/10/06

この章では、Coq で挿入ソートを定義し、定義したソート関数が実際にリストを整列させることを証明します。

次の章では、Extraction という機能を使って、ここで定義した挿入ソートを OCaml や Haskell、Scheme のコードへ変換する方法を紹介します。

証明駆動開発

これまで Coq で色々な関数を定義し、定義した関数の性質を証明してきましたが、実際に Coq を使って安全性の保証されたソフトウェアを開発するところまでは解説しませんでした。

Coq で安全なソフトウェアを開発する流れは、

(1) まず書こうとしているプログラムがどういう性質をみたすべきかを記述し、

(2) Coq でそれをみたすようなプログラムを書き、

(3) 実際に最初に考えた性質を証明し、

(4) Extraction して他の言語のコードに変換する

となります。

このように、プログラムがみたすべき性質に合うようにコーディングし、ソフトウェアを開発するという考え方は「証明駆動」と呼ばれています。

これから二回にわたり、上の流れに沿ってリストをソートする関数をプログラミングしていきます。今回は他のソートアルゴリズムより証明が易しい、挿入ソートを実装します。

今回は (1)、(2)、(3) の段階を紹介し、次回は (4) の Extraction 機能について説明します。

挿入ソートの定義

まずは、(1) の段階です。リストをソートする関数を書こうとしたとき、それがどういう性質を持っているべきか考えてみましょう。

一つは、当たり前のことですが、ソート関数の結果のリストは整列しているという性質です。しかしこれだけではまだソート関数としては不十分で、もう一つの性質として、ソート前のリストとソート後のリストは同じ要素から成っていることが挙げられます。ただし、ここでは「同じ要素から成る」ことは要素が現れる回数も等しいときのみを言います。別の表現をすると、ソート前のリストはソート後のリストの順列になっている、とも言えます。

書こうとしているソート関数の名前を insertion_sort とすると、たとえば、

insertion_sort (2 :: 0 :: 2 :: 4 :: nil) = 0 :: 2 :: 2 :: 4 :: nil

になっていれば insertion_sort は少なくとも引数 (2 :: 0 :: 2 :: 4 :: nil) に対して正しいソートを行っていますが、もし

(a) insertion_sort (2 :: 0 :: 2 :: 4 :: nil) = 0 :: 2 :: 4 :: nil
(b) insertion_sort (2 :: 0 :: 2 :: 4 :: nil) = 0 :: 2 :: 4 :: 2 :: nil

などの結果が得られてしまったら、insertion_sort は正しいソート関数でないと言えます。(a) は insertion_sort の返すリストが元のリストから 2 が一個抜けていて、順列になっていません。(b) は順列にはなっていますが返すリストが整列していませんね。

ソート関数が持つべき性質は、リスト l1、l2 を受け取って「l1 が l2 の並べ替えになっている」ことを表す型と、リスト l を受け取って「l が整列している」ことを表す型があれば表現できます。「順列になっている」ことや「整列している」ことは直感的にはどういうことか分かると思いますが、Coq で表すとどうなるのでしょうか。

まず、あるリストがあるリストと同じ要素から成っていることは Sorting.Permutation モジュールで

Inductive Permutation : list A -> list A -> Prop :=
  | perm_nil: Permutation [] []
  | perm_skip x l l' : Permutation l l' -> Permutation (x::l) (x::l')
  | perm_swap x y l : Permutation (y::x::l) (x::y::l)
  | perm_trans l l' l'' : Permutation l l' -> Permutation l' l'' -> Permutation l l''.

と定義されています。これは言葉で書くと、

(A) nil は nil と同じ要素から成っている

(B) l が l' と同じ要素から成っているとき、x::l は x::l' と同じ要素から成っている

(D) l が l' と同じ要素から成っていて、l' が l'' と同じ要素から成っているとき、l は l'' と同じ要素から成っている

という意味になります。たとえば、リスト (1 :: 2 :: 3 :: nil) と (2 :: 1 :: 3 :: nil) は、(C) によって並べ替えであることが言えます。(1 :: 2 :: 3 :: nil) と (1 :: 3 :: 2 :: nil) はどうかというと、(C) によって (2 :: 3 :: nil) は (3 :: 2 :: nil) と同じ要素から成っていることが分かり、それと (B) により並べ替えであることが分かります。

l と l' を直線で結んで Permutation l l' を表現すれば、上の定義はこのような図になります。これは実線の関係が成り立つときに破線の関係も必ず成り立つと読みます。

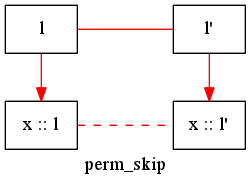
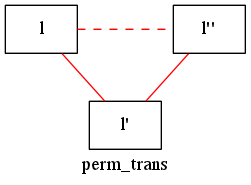
この定義は

任意の値 x に対して、l1 に属する x の数と l2 に属する x の数は等しい

という命題と同値になります。この表現の方が l1 が l2 と同じ要素から成っていることを表すのにしっくり来るかもしれませんが、Permutation の形の方が扱いやすいので今回は Permutation を使うことにします。

次に、リスト l が整列していることは、Sorting.Sorted モジュールで

Inductive LocallySorted (A : Type) (R : A -> A -> Prop) : list A -> Prop :=
    LSorted_nil : LocallySorted R nil
  | LSorted_cons1 : forall a : A, LocallySorted R (a :: nil)
  | LSorted_consn : forall (a b : A) (l : list A),
      LocallySorted R (b :: l) ->
        R a b -> LocallySorted R (a :: b :: l)

(* A は省略 *)

と定義されています。引数の R には le など順序を表す関数を代入して使います。これも言葉で書くと、

nil は整列している

x::nil は整列している

y::l が整列しているとき、R x y ならば x::y::l は整列している

となります。

Permutation と LocallySorted を使うと、insertion_sort が正しいソート関数であるという命題は以下の二つの関数で表せます。

isort_permutation : forall (l : list nat), Permutation l (insertion_sort l)
isort_sorted      : forall (l : list nat), LocallySorted le (insertion_sort l)

任意のリスト l に対し、isort_permutation は l が insertion_sort l と同じ要素から成っていることを表し、isort_sorted は insertion_sort l が整列していることを表します。この二つが証明できれば、insertion_sort は正しいソート関数であることが保証されますね。

では、(2) の段階に入りましょう。証明の対象となる挿入ソートを定義します。

挿入ソートは以下のような手順でリストをソートします。

リストが空なら空を返す
x::xs なら、xs を再帰的にソートし、x をソートされたリストへ順序を保つように挿入する

これを実現するには、順序を保ったまま値を挿入する insert 関数を定義し、それを使ってリストをソートする insertion_sort 関数を定義します。

Require Import List.
Require Import Arith.

Fixpoint insert (a : nat)(l : list nat) : list nat :=
  match l with
  | nil => a :: nil
  | x :: xs => if leb a x then a :: l else x :: insert a xs
  end.

Fixpoint insertion_sort (l : list nat) : list nat :=
  match l with
  | nil => nil
  | x :: xs => insert x (insertion_sort xs)
  end.

leb a x は、a <= x なら true を、そうでなければ false を返す関数でした。よって insert a (x :: xs) は、a <= x ならば a :: x :: xs を返し、そうでなければ x :: insert a xs のように再帰的に a を xs に挿入します。

insert や insertion_sort の実行例を Eval compute in コマンドで見てみましょう。Command Pane で以下のように打ってみてください。

Eval compute in  insert 1 nil

Result for command Eval compute in insert 1 nil . :
     = 1 :: nil
     : list nat

リストが nil のときはそのまま挿入した値のみのリストになりました。

Eval compute in  insert 5 (1 :: 4 :: 2 :: 9 :: 3 :: nil)

Result for command Eval compute in insert 5 (1 :: 4 :: 2 :: 9 :: 3 :: nil) . :
     = 1 :: 4 :: 2 :: 5 :: 9 :: 3 :: nil
     : list nat

1, 4, 2 は 5 以下ですが、9 は 5 より大きいので、2 と 9 の間に 5 が挿入されました。

insertion_sort の動作も見てみましょう。

Eval compute in  insertion_sort (2 :: 4 :: 1 :: 5 :: 3 :: nil)

Result for command Eval compute in insertion_sort (2 :: 4 :: 1 :: 5 :: 3 :: nil) . :
     = 1 :: 2 :: 3 :: 4 :: 5 :: nil
     : list nat

実際にソートされていますね。

挿入ソートの証明

isort_permutation と isort_sorted が成り立つような挿入ソートがソートとして適切だと決め、挿入ソートも実際に定義しました。では (3) の段階に移ります。isort_permutation と isort_sorted を証明してみましょう。isort_permutation と isort_sorted を証明するためにはいくつか補題が必要かもしれないので、insertion_sort の安全性が保証されるまでの流れは以下のようになります。

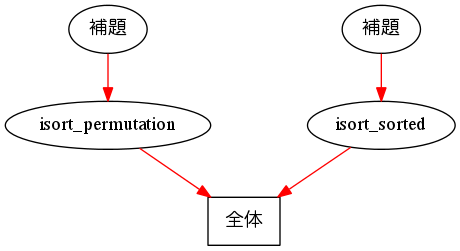
それぞれを証明して行きましょう。

isort_permutation の証明 (1) (補題 insert_perm の証明)

isort_permutation と isort_sorted を証明するために、以下の四つのモジュールをインポートしておきます。

Require Import List.
Require Import Arith.
Require Import Sorting.Permutation.
Require Import Sorting.Sorted.

まずは isort_permutation を証明してみようと思います。いきなり proof-editing mode での証明を始めず、どうやって証明するかを考えてみます。

isort_permutation の型は

forall (l : list nat), Permutation l (insertion_sort l)

でした。帰納法で証明することを考えてみましょう。l が nil のときは insertion_sort l は nil になるので全体は Permutation nil nil となり、自明です。よって l が x :: xs のときを考えてみます。

仮定に

Permutation xs (insertion_sort xs)

が追加され、insertion_sort (x::xs) は "insert x (insertion_sort xs)" と簡約され、示すことは Permutation (x::xs) (insert x (insertion_sort xs)) となります。もしここで

(a) Permutation (x :: xs) (x :: insertion_sort xs)
(b) Permutation (x :: insertion_sort xs) (insert x (insertion_sort xs))

が示されたとすると、Permutation のコンストラクタである

perm_trans : forall l l' l'', Permutation l l' -> Permutation l' l'' -> Permutation l l''.

の l に x :: xs、l' に x :: insertion_sort xs、l'' に (insert x (insertion_sort xs)) を当てはめると、

Permutation (x :: xs) (x :: insertion_sort xs) ->
  Permutation (x :: insertion_sort xs) (insert x (insertion_sort xs)) ->
    Permutation (x :: xs) (insert x (insertion_sort xs))

となり、これを使って "Permutation (x::xs) (insert x (insertion_sort xs))" を示せます。(a) は、帰納法の仮定 "Permutation xs (insertion_sort xs)" と Permutation のコンストラクタ

perm_skip : forall x l l', Permutation l l' -> Permutation (x :: l) (x :: l')

を使えば証明できるので、(b) を補題として証明してから全体を証明します。

ここでは、(b) の "insertion_sort xs" の部分を変数 l で置き替えた形の命題を proof-editing mode で証明しようと思います。(b) を insert_sorted という名前にすれば、今は下図の色の付いたところを証明しようとしていることになります。

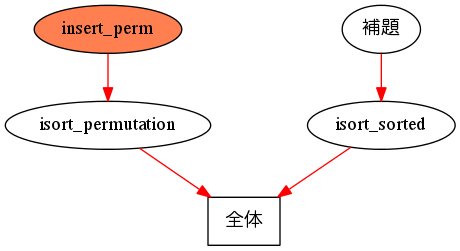
insert_perm の証明を始めましょう。

Lemma insert_perm : forall (x : nat)(l : list nat), Permutation (x :: l) (insert x l).

1 subgoal
______________________________________(1/1)
forall (l : list nat) (x : nat), Permutation (x :: l) (insert x l)

l についての帰納法で示すので、induction を使ってみます。

induction l.

2 subgoals
______________________________________(1/2)
forall x : nat, Permutation (x :: nil) (insert x nil)

______________________________________(2/2)
forall x : nat, Permutation (x :: a :: l) (insert x (a :: l))

一つ目のサブゴールを intro して simpl してみます。

intro.
simpl.

2 subgoals
x : nat
______________________________________(1/2)
Permutation (x :: nil) (x :: nil)

______________________________________(2/2)
forall x : nat, Permutation (x :: a :: l) (insert x (a :: l))

x :: nil は明らかに x :: nil と同じ要素から成っていますね。

すべてのリスト l に対して、l が l と同じ要素から成っているという定理は

Permutation_refl : forall (A : Type)(l : list A), Permutation l l

という名前で Sorting.Permutation モジュールで用意されています。これを使って一つ目のサブゴールを示しましょう。

apply Permutation_refl.

1 subgoal
a : nat
l : list nat
IHl : forall x : nat, Permutation (x :: l) (insert x l)
______________________________________(1/1)
forall x : nat, Permutation (x :: a :: l) (insert x (a :: l))

intro して simpl してみましょう。

intro.
simpl.

1 subgoal
a : nat
l : list nat
IHl : forall x : nat, Permutation (x :: l) (insert x l)
x : nat
______________________________________(1/1)
Permutation (x :: a :: l) (if leb x a then x :: a :: l else a :: insert x l)

サブゴールに "if leb x a then" が現れたので、destruct タクティクで "leb x a" を場合分けします。

destruct (leb x a).

2 subgoals
a : nat
l : list nat
IHl : forall x : nat, Permutation (x :: l) (insert x l)
x : nat
______________________________________(1/2)
Permutation (x :: a :: l) (x :: a :: l)

______________________________________(2/2)
Permutation (x :: a :: l) (a :: insert x l)

一つ目のサブゴールは先程使った Permutation_refl で証明できますね。

apply Permutation_refl.

1 subgoal
a : nat
l : list nat
IHl : forall x : nat, Permutation (x :: l) (insert x l)
x : nat
______________________________________(1/1)
Permutation (x :: a :: l) (a :: insert x l)

一つ目のサブゴールが証明されました。

ここで、

Permutation (x :: a :: l) (a :: x :: l)

が "perm_swap : forall x y l, Permutation (y :: x :: l) (x :: y :: l)" から言え、

Permutation (a :: x :: l) (a :: insert x l)

が IHl と "perm_skip : forall x l l', Permutation l l' -> Permutation (x :: l) (x :: l')" を使うと言えるので、"perm_trans : forall l l' l'', Permutation l l' -> Permutation l' l'' -> Permutation l l''" を使うとこのサブゴールは証明できます。

しかし perm_trans を apply しようとすると、

apply perm_trans.

Error: Unable to find an instance for the variable l'.

とエラーになってしまいます。これは、サブゴールを見ると l、l'' はそれぞれ (x :: a :: l)、(a :: insert x l) であることが推論されますが、l' が何なのかは Coq には分からないので、エラーになってしまいます。かといって、引数を渡してやると

apply (perm_trans (x :: a :: l) (a :: x :: l) (a :: insert x l)).

Error:
In environment
a : nat
l : list nat
IHl : forall x : nat, Permutation (x :: l) (insert x l)
x : nat
The term "a :: x :: l" has type "list nat" while it is expected to have type
 "Permutation ?6367 ?6368".

のようにまたエラーになってしまいます。perm_trans の定義を Command Pane で見てみると

Print Permutation_trans

Result for command Print perm_trans . :
Inductive Permutation (A : Type) : list A -> list A -> Prop :=
    perm_nil : Permutation nil nil
  | perm_skip : forall (x : A) (l l' : list A),
          Permutation l l' -> Permutation (x :: l) (x :: l')
  | perm_swap : forall (x y : A) (l : list A),
          Permutation (y :: x :: l) (x :: y :: l)
  | perm_trans : forall l l' l'' : list A,
          Permutation l l' -> Permutation l' l'' -> Permutation l l''

For Permutation: Argument A is implicit
For perm_skip: Arguments A, l, l' are implicit
For perm_swap: Argument A is implicit
For perm_trans: Arguments A, l, l', l'' are implicit    (* ! *)
...

とあり、(* ! *) を付けた行にあるように l、l'、l'' は省略されていると Coq が判断するのでエラーになってしまうのです。そこで、apply ... with ... というタクティクを使います。

apply perm_trans with (a :: x :: l).

2 subgoals
a : nat
l : list nat
IHl : forall x : nat, Permutation (x :: l) (insert x l)
x : nat
______________________________________(1/2)
Permutation (x :: a :: l) (a :: x :: l)

______________________________________(2/2)
Permutation (a :: x :: l) (a :: insert x l)

エラーが出ずに apply できました。

apply X with p は今回のように、Coq が X の中の変数を推論できないときに使え、推論できなかった変数に p を与えます。

これで証明が進みそうですね。まず一つ目のサブゴールは perm_swap で証明できます。

apply perm_swap.

1 subgoal
a : nat
l : list nat
IHl : forall x : nat, Permutation (x :: l) (insert x l)
x : nat
______________________________________(1/1)
Permutation (a :: x :: l) (a :: insert x l)

一つ目のサブゴールが証明されました。次は、perm_skip と IHl で証明できます。

apply perm_skip.

1 subgoal
a : nat
l : list nat
IHl : forall x : nat, Permutation (x :: l) (insert x l)
x : nat
______________________________________(1/1)
Permutation (x :: l) (insert x l)

Permutation に渡されている二つのリストの先頭の a が消えました。これで IHl を apply すれば証明終了です。

apply IHl.

Proof completed.

isort_permutation の証明 (2)

insert_perm が示せたので、次は isort_permutation の証明です。

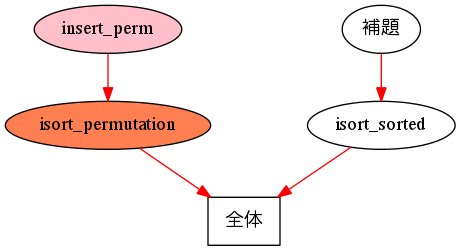
今度は insert_perm を使って、 insertion_sort した結果が元のリストと同じ要素から成っていることを証明します。

Theorem isort_permutation : forall (l : list nat), Permutation l (insertion_sort l).

1 subgoal
______________________________________(1/1)
forall l : list nat, Permutation l (insertion_sort l)

l に関して帰納法で証明します。

induction l.

2 subgoals
______________________________________(1/2)
Permutation nil (insertion_sort nil)

______________________________________(2/2)
Permutation (a :: l) (insertion_sort (a :: l))

一つ目のサブゴールは、insertion_sort nil が nil に簡約されるので perm_nil で証明できます。

apply perm_nil.

1 subgoal
a : nat
l : list nat
IHl : Permutation l (insertion_sort l)
______________________________________(1/1)
Permutation (a :: l) (insertion_sort (a :: l))

apply perm_nil でなくても、constructor タクティクを使っても同じ動作をします。apply perm_nil の読み込みを戻して、constructor を使ってみます。

constructor.

1 subgoal
a : nat
l : list nat
IHl : Permutation l (insertion_sort l)
______________________________________(1/1)
Permutation (a :: l) (insertion_sort (a :: l))

ちゃんと証明できてますね。

次のサブゴールは、まず simpl してみます。

simpl.

1 subgoal
a : nat
l : list nat
IHl : Permutation l (insertion_sort l)
______________________________________(1/1)
Permutation (a :: l) (insert a (insertion_sort l))

ここで、Permutation (a :: l) (a :: insertion_sort l) が IHl と perm_skip から証明でき、Permutation (a :: insertion_sort l) (insert a (insertion_sort l)) は先程示した insert_perm から証明できるので、perm_trans を使ってこのサブゴールが示せます。

apply perm_trans with (a :: insertion_sort l).

2 subgoals
a : nat
l : list nat
IHl : Permutation l (insertion_sort l)
______________________________________(1/2)
Permutation (a :: l) (a :: insertion_sort l)

______________________________________(2/2)
Permutation (a :: insertion_sort l) (insert a (insertion_sort l))

サブゴールが二つに分かれました。一つ目のサブゴールを perm_skip すると IHl の型そのままになります。

apply perm_skip.

2 subgoals
a : nat
l : list nat
IHl : Permutation l (insertion_sort l)
______________________________________(1/2)
Permutation l (insertion_sort l)

______________________________________(2/2)
Permutation (a :: insertion_sort l) (insert a (insertion_sort l))

これで IHl をそのまま apply すれば証明できますね。

apply IHl.

1 subgoal
a : nat
l : list nat
IHl : Permutation l (insertion_sort l)
______________________________________(1/1)
Permutation (a :: insertion_sort l) (insert a (insertion_sort l))

次のサブゴールは insert_perm そのままです。

apply insert_perm.

Proof completed.

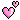
以下に証明の全体書きます。

Lemma insert_perm : forall (l : list nat)(x : nat), Permutation (x::l) (insert x l).
induction l.
 simpl.
 intro.
 apply Permutation_refl.

 intro.
 simpl.
 destruct (leb x a).
  apply Permutation_refl.

  apply perm_trans with (a :: x :: l).
   apply perm_swap.

   apply perm_skip.
   apply IHl.
 Qed.

Theorem isort_permutation : forall (l : list nat), Permutation l (insertion_sort l).
induction l.
 constructor.

  simpl.
  apply perm_trans with (a::insertion_sort l).
   apply perm_skip.
   apply IHl.
   apply insert_perm.
Qed.

isort_sorted の証明 (1) (補題 insert_sorted の証明)

挿入ソート後のリストが元のリストと同じ要素から成っていることは証明できたので、次はソート後のリストが整列していることを証明します。

今度もまずはどうやって証明するか、proof-editing mode に入らずにまず頭で考えてみます。

ソート後のリストが整列しているという命題は、以下のように表せました。

isort_sorted : forall (l : list nat), LocallySorted le (insertion_sort l)

帰納法での証明を考えてみます。まず l が nil の場合は、insertion_sort nil = nil となり、LSorted_nil : LocallySorted le nil から明かです。

"LocallySorted le (insertion_sort l) -> LocallySorted le (insertion_sort (a :: l)" はどうでしょう。LocallySorted le (insertion_sort (a :: l)) は簡約すると

LocallySorted le (insert a (insertion_sort l))

となります。ここで、帰納法の仮定から insertion_sort l は整列していることが分かるので、補題として、l が整列していれば任意の値 a に対して insert a l が整列しているという命題、

insert_sorted : forall (a : nat)(l : list nat), LocallySorted le l -> LocallySorted le (insert a l)

が示されていれば、l に insertion_sort l を代入すれば全体が証明できます。ではまずこれを示してみましょう。

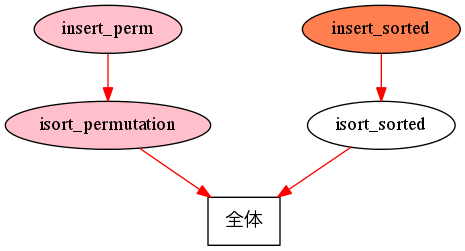
Lemma insert_sorted : forall (a : nat)(l : list nat),
  LocallySorted le l -> LocallySorted le (insert a l).

1 subgoal
______________________________________(1/1)
forall (a : nat) (l : list nat),
LocallySorted le l -> LocallySorted le (insert a l)

l についての帰納法で証明してみます。

induction l.

2 subgoals
a : nat
______________________________________(1/2)
LocallySorted le nil -> LocallySorted le (insert a nil)

______________________________________(2/2)
LocallySorted le (a0 :: l) -> LocallySorted le (insert a (a0 :: l))

insert a nil は a :: nil に簡約されるので、LocallySorted のコンストラクタである LSorted_cons1 : forall (a : nat), LocallySorted le (a :: nil) から示せます。ですから constructor タクティクを使います。

constructor.

1 subgoal
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
______________________________________(1/1)
LocallySorted le (a0 :: l) -> LocallySorted le (insert a (a0 :: l))

一つ目のサブゴールが証明されました。

今度のサブゴールは、まず intros して simpl してみます。

intro.
simpl.

1 subgoal
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
______________________________________(1/1)
LocallySorted le (if leb a a0 then a :: a0 :: l else a0 :: insert a l)

leb a a0 が true か false かで結果が変わってくるので、destruct (leb a a0) で場合分けしたいところですが、そうしてしまうと leb a a0 が true か false かの情報が失われてしまうので、まず remember タクティクで leb a a0 を別の変数で置きます。

remember (leb a a0).

1 subgoal
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
b : bool
Heqb : b = leb a a0
______________________________________(1/1)
LocallySorted le (if b then a :: a0 :: l else a0 :: insert a l)

leb a a0 が b で置き換わりました。 b を destruct します。

destruct b.

2 subgoals
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : true = leb a a0
______________________________________(1/2)
LocallySorted le (a :: a0 :: l)

______________________________________(2/2)
LocallySorted le (a0 :: insert a l)

if での条件分岐が消え、サブゴールが扱いやすくなりました。一つ目のサブゴールは、H と Heqb から LSorted_consn を使えば証明できます。

apply LSorted_consn.

3 subgoals
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : true = leb a a0
______________________________________(1/3)
LocallySorted le (a0 :: l)

______________________________________(2/3)
a <= a0

______________________________________(3/3)
LocallySorted le (a0 :: insert a l)

一つ目のサブゴールは仮定の H の型そのままです。

apply H.

2 subgoals
a : nat
a0 : nat
l : list nat
IHl :  LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : true = leb a a0
______________________________________(1/2)
a <= a0

______________________________________(2/2)
LocallySorted le (a0 :: insert a l)

今度のサブゴールは、仮定に "Heqb : true = leb a a0" があるのでこれを使えば示せそうですね。実際、Arith モジュールで

leb_complete : forall m n : nat, leb m n = true -> m <= n

という定理が用意されているので、これをサブゴールに apply してみましょう。

apply leb_complete.

2 subgoals
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : true = leb a a0
______________________________________(1/2)
leb a a0 = true

______________________________________(2/2)
LocallySorted le (a0 :: insert a l)

Heqb の右辺と左辺を引っくり返しただけのサブゴールになったので、congruence タクティクで自動的に示します。

congruence.

1 subgoal
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : false = leb a a0
______________________________________(1/1)
LocallySorted le (a0 :: insert a l)

一つ目のサブゴールが示せました。

仮定の H は inversion タクティクによって LSorted_cons1 の場合と LSorted_consn の場合に分けれられます。

inversion H.

2 subgoals
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : false = leb a a0
a1 : nat
H1 : a1 = a0
H2 : nil = l
______________________________________(1/2)
LocallySorted le (a0 :: insert a nil)

______________________________________(2/2)
LocallySorted le (a0 :: insert a (b :: l0))

simpl してみます。

simpl.

2 subgoals
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : false = leb a a0
a1 : nat
H1 : a1 = a0
H2 : nil = l
______________________________________(1/2)
LocallySorted le (a0 :: a :: nil)

______________________________________(2/2)
LocallySorted le (a0 :: insert a (b :: l0))

Heqb と LSorted_consn から証明できそうです。

apply LSorted_consn.

3 subgoals
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : false = leb a a0
a1 : nat
H1 : a1 = a0
H2 : nil = l
______________________________________(1/3)
LocallySorted le (a :: nil)

______________________________________(2/3)
a0 <= a

______________________________________(2/2)
LocallySorted le (a0 :: insert a (b :: l0))

最初のサブゴールは LSorted_cons1 をそのまま apply すれば示せます。

apply LSorted_cons1.

2 subgoals
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : false = leb a a0
a1 : nat
H1 : a1 = a0
H2 : nil = l
______________________________________(1/2)
a0 <= a

______________________________________(2/2)
LocallySorted le (a0 :: insert a (b :: l0))

一つ目のサブゴールが証明されました。

今度は、サブゴールを上手く変形して Heqb の形にできれば示せそうです。Arith モジュールには以下の定理が用意されているので、これらを使います。

lt_le_weak : forall n m : nat, n < m -> n <= m
leb_complete_conv : forall n m : nat, leb m n = false -> n < m

lt_le_weak を apply すればサブゴールが a < a0 になり、そこに leb_complete_conv を apply すればサブゴールが leb a0 a = false になるので、Heqb の右辺と左辺を入れ替えた形になります。

apply lt_le_weak.
apply leb_complete_conv.

2 subgoals
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : false = leb a a0
a1 : nat
H1 : a1 = a0
H2 : nil = l
______________________________________(1/2)
leb a a0 = false

______________________________________(2/2)
LocallySorted le (a0 :: insert a (b :: l0))

また congruence タクティクで示します。

congruence.

1 subgoal
a : nat
a0 : nat
l : list nat
IHl : LocallySorted le l -> LocallySorted le (insert a l)
H : LocallySorted le (a0 :: l)
Heqb : false = leb a a0
a1 : nat
b : nat
l0 : list nat
H2 : LocallySorted le (b :: l0)
H3 : a0 <= b
H0 : a1 = a0
H1 : b :: l0 = l
______________________________________(1/1)
LocallySorted le (a0 :: insert a (b :: l0))

サブゴールが一つ消えました。仮定に "H0 : a1 = a0" や "H1 : b :: l0 = l" など等式が現れているので、subst タクティクで整理します。

subst.

1 subgoal
a : nat
a0 : nat
Heqb : false = leb a a0
b : nat
l0 : list nat
H2 : LocallySorted le (b :: l0)
H3 : a0 <= b
IHl : LocallySorted le (b :: l0) -> LocallySorted le (insert a (b :: l0))
H : LocallySorted le (a0 :: b :: l0)
______________________________________(1/1)
LocallySorted le (a0 :: insert a (b :: l0))

サブゴールと IHl は insert を簡約できるので、simpl タクティクを使ってみます。

simpl.
simpl in IHl.

1 subgoal
a : nat
a0 : nat
Heqb : false = leb a a0
b : nat
l0 : list nat
H2 : LocallySorted le (b :: l0)
H3 : a0 <= b
IHl : LocallySorted le (b :: l0) ->
      LocallySorted le (if leb a b then a :: b :: l0 else b :: insert a l0)
H : LocallySorted le (a0 :: b :: l0)
______________________________________(1/1)
LocallySorted le (a0 :: (if leb a b then a :: b :: l0 else b :: insert a l0))

また leb a b で場合分けできるので、remember タクティクで別の変数で置いてから destruct します。

remember (leb a b).

1 subgoal
a : nat
a0 : nat
Heqb : false = leb a a0
b : nat
l0 : list nat
H2 : LocallySorted le (b :: l0)
H3 : a0 <= b
b0 : bool
Heqb0 : b0 = leb a b
IHl : LocallySorted le (b :: l0) ->
      LocallySorted le (if b0 then a :: b :: l0 else b :: insert a l0)
H : LocallySorted le (a0 :: b :: l0)
______________________________________(1/1)
LocallySorted le (a0 :: (if b0 then a :: b :: l0 else b :: insert a l0))

Heqb0 : b0 = leb a b が現れたので、b0 を destruct します。

destruct b0.

2 subgoals
a : nat
a0 : nat
Heqb : false = leb a a0
b : nat
l0 : list nat
H2 : LocallySorted le (b :: l0)
H3 : a0 <= b
Heqb0 : true = leb a b
IHl : LocallySorted le (b :: l0) -> LocallySorted le (a :: b :: l0)
H : LocallySorted le (a0 :: b :: l0)
______________________________________(1/2)
LocallySorted le (a0 :: a :: b :: l0)

______________________________________(2/2)
LocallySorted le (a0 :: b :: insert a l0)

サブゴールが二つに分かれました。

IHl と H2 から "LocallySorted le (a :: b :: l0)" が導かれ、Heqb から "a0 <= a" を導けば一つ目のサブゴールが LSorted_consn から示せます。

apply LSorted_consn.

3 subgoals
a : nat
a0 : nat
Heqb : false = leb a a0
b : nat
l0 : list nat
H2 : LocallySorted le (b :: l0)
H3 : a0 <= b
Heqb0 : true = leb a b
IHl : LocallySorted le (b :: l0) -> LocallySorted le (a :: b :: l0)
H : LocallySorted le (a0 :: b :: l0)
______________________________________(1/3)
LocallySorted le (a :: b :: l0)


______________________________________(2/3)
a0 <= a

______________________________________(3/3)
LocallySorted le (a0 :: b :: insert a l0)

一つ目のサブゴールが "LocallySorted le (a :: b :: l0)" と "a0 <= a" に分かれました。分岐後の最初のサブゴールは IHl と H2 で示します。

apply IHl.
apply H2.

2 subgoals
a : nat
a0 : nat
Heqb : false = leb a a0
b : nat
l0 : list nat
H2 : LocallySorted le (b :: l0)
H3 : a0 <= b
Heqb0 : true = leb a b
IHl : LocallySorted le (b :: l0) -> LocallySorted le (a :: b :: l0)
H : LocallySorted le (a0 :: b :: l0)
______________________________________(1/2)
a0 <= a

______________________________________(2/2)
LocallySorted le (a0 :: b :: insert a l0)

次は、先程使った定理 lt_le_weak と leb_complete_conv で示せます。lt_le_weak と leb_complete_conv は以下のような定理でした。

lt_le_weak : forall n m : nat, n < m -> n <= m
leb_complete_conv : forall n m : nat, leb m n = false -> n < m

これらを apply して示します。

apply lt_le_weak.
apply leb_complete_conv.
congruence.

1 subgoal
a : nat
a0 : nat
Heqb : false = leb a a0
b : nat
l0 : list nat
H2 : LocallySorted le (b :: l0)
H3 : a0 <= b
Heqb0 : false = leb a b
IHl : LocallySorted le (b :: l0) -> LocallySorted le (b :: insert a l0)
H : LocallySorted le (a0 :: b :: l0)
______________________________________(1/1)
LocallySorted le (a0 :: b :: insert a l0)

最後のサブゴールになりました。今度も IHl と H2 から "LocallySorted le (b :: insert a l0)" を導き、"H3 : a0 <= b" を使って LSorted_consn から証明できます。

apply LSorted_consn.
 apply IHl.
 apply H2.

 apply H3.

Proof completed.

isort_sorted の証明 (2)

insert_sorted を使って、isort_sorted を証明します。

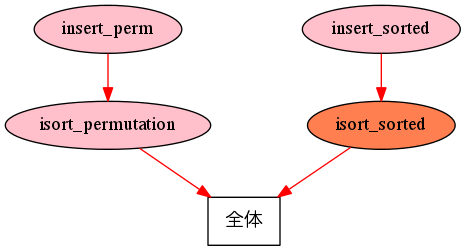
Theorem isort_sorted : forall (l : list nat), LocallySorted le (insertion_sort l).

1 subgoal
______________________________________(1/1)
forall l : list nat, LocallySorted le (insertion_sort l)

l についての帰納法で示します。

induction l.

2 subgoals
______________________________________(1/2)
LocallySorted le (insertion_sort nil)

______________________________________(2/2)
LocallySorted le (insertion_sort (a :: l))

insertion_sort nil は nil に簡約され、LSorted_nil で証明できるので、constructor タクティクで一度に示します。

constructor.

1 subgoal
a : nat
l : list nat
IHl : LocallySorted le (insertion_sort l)
______________________________________(1/1)
LocallySorted le (insertion_sort (a :: l))

一つ目のサブゴールが消えました。今度は、まずは simpl してみます。

simpl.

1 subgoal
a : nat
l : list nat
IHl : LocallySorted le (insertion_sort l)
______________________________________(1/1)
LocallySorted le (insert a (insertion_sort l))

仮定の IHl から、insert_sorted を使えばそのまま証明できますね。

apply insert_sorted.
apply IHl.

Proof completed.

isort_sorted も証明できました。isort_permutation、insertion_sort が示されたことにより、insertion_sort は正しいソート関数になっていることが保証されました。

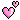
証明の全体書いておきます。

Lemma insert_sorted : forall (a : nat)(l : list nat),
    LocallySorted le l -> LocallySorted le (insert a l).
induction l.
 constructor.

 intro.
 simpl.
 remember (leb a a0).
 destruct b.
  apply LSorted_consn.
  apply H.
  apply leb_complete.
  congruence.

  inversion H.
  simpl.
  apply LSorted_consn.
  apply LSorted_cons1.
  apply lt_le_weak.
  apply leb_complete_conv.
  congruence.

  subst.
  simpl.
  simpl in IHl.
  remember (leb a b).
  destruct b0.
   apply LSorted_consn.
   apply IHl.
   apply H2.

   apply lt_le_weak.
   apply leb_complete_conv.
   congruence.

  apply LSorted_consn.
  apply IHl.
  apply H2.
  apply H3.
Qed.

Theorem isort_sorted : forall (l : list nat), LocallySorted le (insertion_sort l).
induction l.
 constructor.

 simpl.
 apply insert_sorted.
 apply IHl.
Qed.

先程述べたように、次回は Coq で書いたコードを他の言語のコードに変換する方法を紹介します。これで、Coq でプログラムを書く一連の流れが紹介されるので、楽しみにしてください。

前回の練習問題の答え

問題はこうでした。

問12. nat の二重リストを受け取って、与えられたリストが

(a11 :: a12 :: ... :: a1n :: nil) ::
(a21 :: a22 :: ... :: a2n :: nil) ::
...
(am1 :: am2 :: ... :: amn :: nil) :: nil

のとき

(a11 :: a21 :: ... :: am1 :: nil) ::
(a12 :: a22 :: ... :: am2 :: nil) ::
...
(a1m :: an2 :: ... :: anm :: nil) :: nil

を返す関数 transpose を定義しなさい。ただし引数が nil のときは nil を返し、内側のそれぞれのリストの長さが異なるとき、つまり

(a11 :: a12 :: a13 :: nil) ::
(a21 :: a22 :: a23 :: a24 :: nil) ::
(a31 :: a32 :: nil) :: nil

のようなときは、

(a11 :: a21 :: a31 :: nil) ::
(a12 :: a22 :: a32 :: nil) ::
(a13 :: a24 :: 0   :: nil) :: nil

のように、先頭のリストに長さを合わせて計算するものとします。

答えの一例を挙げます。

Require Import List.
Require Import Arith.
Require Import Recdef.

Function transpose (l : list (list nat)) {measure (fun l => length (hd nil l)) l} : list (list nat) :=
  match l with
  | nil => nil
  | nil::_ => nil
  | (x::xs)::xss => map (hd 0) l :: transpose (map (@tl nat) l)
  end.
Proof.
(*
  length (hd nil (map tl ((x :: xs) :: xss))) <
  length (hd nil ((x :: xs) :: xss))
 *)
simpl.
intros.
subst.
induction xs.
 constructor.

 constructor.
Defined.

ここで使った関数は以下の通りです。

Fixpoint map (A B : Type)(f : A -> B)(l:list A) : list B :=
  match l with
  | nil => nil
  | a :: t => f a :: map f t
  end.

Definition hd (A : Type)(default:A) (l:list A) :=
    match l with
      | nil => default
      | x :: _ => x
    end.

Definition tl (A : Type)(l:list A) :=
    match l with
      | nil => nil
      | a :: m => m
    end.

(* ただし、A、B は省略 *)

プログラミング Coq

証明駆動開発入門(1)