Coq を始めよう

このチュートリアルでは定理証明支援系言語である Coq について解説をします。プログラムの性質を Coq で証明できるようになることが目標です。

読者の前提知識としては OCaml や Haskell などの関数型言語でプログラミングできることを想定します。また、本文書において Coq のプログラムとの比較には Haskell と OCaml を用いますが、Haskell や OCaml を書いたことがなくても他の関数型言語に触れていれば理解できるような内容を心がけます。そして、数学に精通している必要はありません。話の中でどうしても数学的な内容に踏み込むことがありますが、そこでは簡単に説明しますので、数学が苦手という方も少しずつ順を追って理解していってください。

Coq とは何か?

Coq は定理証明支援系言語です。定理証明、と聞いて皆さんは何を思い浮かべるでしょうか。多くの人は「数学」の二文字を連想し、「プログラミングは好きだけど数学はちょっと……」と思って積極的な気持ちを持たないかもしれません。 しかし、Coq の用途は数学の定理を証明することにも使われますが、むしろプログラムの正しさを保証したり、安全なプログラムを書く、といった用途で使われます。筆者は数学が好きで Coq に興味を持ったため、遊び感覚で数学の上の簡単な定理を示したりすることもあります。ただ、プログラムの証明を書くことの方が多く、そのときは数学と Coq は切り離して考えています。

ではプログラムの正しさを保証することにはどんな意味があるのでしょうか。テストをするだけでは何が足りないのでしょうか。たとえば、テストでは検査すべき状態が膨大になり、たくさんのテストケースが必要になる場合がありますが、もし証明できるのであれば証明は一回で十分です。このようにテストでなく証明が有用なケースがあり、実際にも利用されています。

具体的に Coq で安全性の示されたツールの例としては、最適化が正しくされていることを保証した C 言語コンパイラである CompCert があります。また、iZE Smart Desktop では、D-Bus で扱うデータと JSON との相互変換の正しさが証明されています。

なんだかおおげさな話になってしまいました。筆者としては、読者のみなさんが Coq による定理証明を難しいことだと引いて構えるのではなく、パズルを解く感覚で楽しんでもらいたいと思っています。

ではこれから一緒に楽しく Coq を学んでいきましょう。

環境を整える

Coq は 公式サイト の右上に見える Get Coq からダウンロードできます。この連載では、Coq のバージョンを 8.3 だと仮定して話を進めます。8.2 だと、チュートリアルの内容と合わない部分があるので、必ず 8.3 を使って下さい。

この連載では、Coq に加えて、Coq の統合環境である CoqIDE を使います。インストールの方法は以下の通りです。

Mac の場合

coq-8.3pl1-macosx.dmg と coqide-8.3pl1-macosx.dmg の両方をダウンロードしてインストールしてください。/usr/local にインストールされます。

Debian や Ubuntu の場合

 # sudo apt-get install coq coqide

でインストールできます。

Windows の場合

coq-8.3pl1-win-0.exe をダウンロードしてインストールしてください。

ソースコードからインストールする場合

ソースコードからインストールをするには、 Coq は OCaml で開発されているため OCaml、camlp5 もインストールする必要があります。OCaml は ここ からダウンロードでき、camlp5 は ここ からダウンロードできます。

前述した通り本文書では CoqIDE を使うことを前提としますが、他にもコンソールで対話的に証明ができる coqtop や、Coq 以外にも様々な定理証明言語に対している、Emacs をインターフェースとした Proof General というツールもあります。筆者は簡単な命題をちょこっと証明したいときには coqtop を使うことがあります。そして、Emacs 使いには Proof General は使いやすいでしょう。

Coq で関数を書く

インストールが済んだら早速 Coq に触れてみましょう。

それでは、CoqIDE を立ち上げてみましょう。こんなウィンドウが表示されたでしょうか。

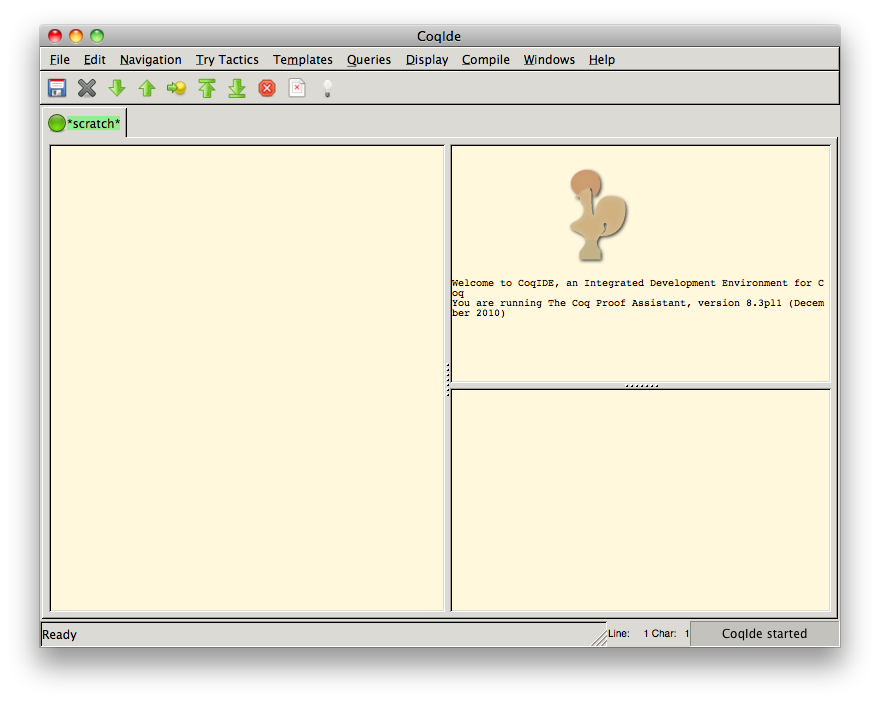
左にある大きな枠が証明やプログラムを記述するスペースです。ニワトリの絵がある右上の枠は、証明の途中において現在の仮定と結論の状態を表示するスペースですが、詳しいことは次回解説します。そして、右下のスペースはエラーや成功などのメッセージを表示するスペースです。

まずは Coq で証明ではなく簡単なプログラムを書いてみましょう。なぜまずプログラムなのかというと、次の節で説明しますが、プログラムを書くことは証明することにそのまま繋がってくるからです。

最初から表示されている "*scratch*" と書かれたタブにプログラムを書くと使い捨てのプログラムになります。ただし、後からファイルに保存することもできます。また、左上の "File" から "New" を選択すると新規にファイルを生成できるので、それを編集していってもよいです。

Coq のプログラムの拡張子は ".v" にすることが好まれます。

準備が整ったら、早速 Coq で簡単な関数を書いてみます。関数を定義するには Definition を使います。たとえば、自然数を二つ受け取ってそれらを足す関数 plus は次のように書きます。

(* 二つの自然数の和を返す *)
Definition plus (n : nat)(m : nat) : nat := n + m.

"(*" と "*)" に囲まれた部分はコメントになります。

Coq では改行やタブは意味を持たず、"." までが一つの文です。Definition の後には関数名(識別子)が続きます。この例ではplus は関数名です。Haskell や OCaml を書いたことがある方なら推測できるかもしれませんが、"(n : nat)(m : nat) : nat" の部分は「型が nat である引数 n と m を取り戻り値の型が nat である」ことを示しています。そして、:= の後の n + m は関数本体の定義部分になります。nat は自然数の型で、0, 1, 2, ... が含まれます(Coq では自然数は 0 を含んで定義されます)。

今回は n と m の型は同じなので、簡単に次のように書くこともできます。

Definition plus (n m : nat) : nat := n + m.

二つの ": nat" は暗黙の型推論により省略できます。

Definition plus n m := n + m.

Coq で識別子には、一文字目には英字、下線( _ )と Unicode で識別子として利用可能とされている文字、二文字目以降はその他に数字やプライム( ' )が使えます。識別子として使えない予約語は以下の通りです。

as	at	cofix	else	end
exists	exists2	fix	for	forall
fun	if	IF	in	let
match	mod	Prop	return	Set
then	Type	using	where	with
_

では、プログラムを書いて CoqIDE に読み込ませてみましょう。右上に緑色の矢印が並んでいますが、その中の左端にある下向きの矢印を選択してみてください。"Definition" から "." までの背景が緑色に変わりましたか? 背景色が緑色になって、右下の枠に "plus is defined" と表示されていたら成功です。plus は IDE に読み込まれました。もし背景色が変わらず、右下の枠にエラーが表示されていたら打ち間違えの可能性があります。

定義した関数に具体的な値を入れて戻り値を確かめてみましょう。メニューバーにある "Windows" から "Show/Hide Query Pane" を選択してください。 ウィンドウの下に "Command Pane" を書かれた新しい枠ができましたね。さらにこの枠の左側にボタンが3個あり、そのうち真ん中にある、白い紙が書かれたボタンを選択してみてください。Page 1 と書かれたタブとテキストボックスが二つ現れました。ここで色々なコマンドが実行できます。たとえば plus に 3 と 5 を適用した結果を見たい場合は左側のテキストボックスに

Eval compute in

と打ち、右側のテキストボックスには

plus 3 5

と打ちます。

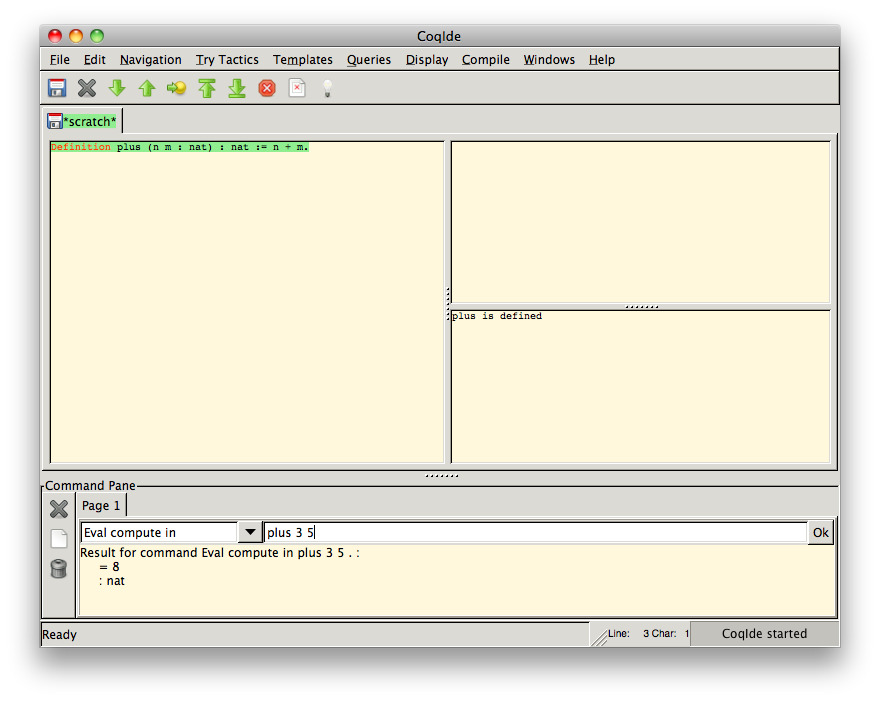
Ok ボタンまたはリターンキーを押すと

Result for command Eval compute in plus 3 5.:
   = 8
   : nat

と表示されたでしょうか。見て分かるようにこれが plus に 3 と 5 を渡した結果です。

また、plus は無名関数を使って次のように書くこともできます。

Definition plus' : nat -> nat -> nat := fun n m => n + m.

Coq で x を引数として y を返す無名関数は "fun x => y" のように fun の後に引数、=> の後に関数本体の定義を書きます。これは Haskell では "\x -> y" 、OCaml では "fun x -> y" に相当します。上のように複数の引数を持つ場合は、"fun a b c => d" のようにスペースで区切って複数の引数を書きます。":=" の左側の "nat -> nat -> nat" は自然数を二つ取って自然数を返す関数の型です。

次に、もっと単純に、「x を取ると x をそのまま返す関数 id」を定義してみましょう。id は次のように書くことができます。

Definition id (A : Type)(x : A) : A := x.

Type という何やら新しい文字列が見えますね。Type とは型の型の一つで、Coq でのあらゆる型を内包します。これで "A : Type" は型 A の型が Type である、ということを意味するのが分かります。A は Haskell でいう型変数で、nat などの具体的な型ではないので、気を付けましょう。Haskell で書くと、こうなります。

id :: a -> a
id x = x

型の型はソートと呼ばれています。「整列」の意味のソートとは無関係なので注意してください。

型変数の名前は大文字から始めることが一般的ですが、小文字から始めてもエラーにはなりません。また、ソートは Type、Prop、Set の三種類ありますが、どれも大文字で始まります。関数名は this_is_a_function のようにアンダースコアで区切った記法を使うのが一般的です。これも記法や大文字小文字の違いによってエラーになることはありません。

先程 plus に二種類の書き方ができたように、id も無名関数を使って定義できます。

Definition id' : forall (A : Type), A -> A := fun A x => x.

forall は全称量化子と呼ばれ、"id : forall (A : Type), A -> A" は id の型が「型が Type である任意の型 A に対して A -> A」だということを表します。数学の用語だと少しややこしく感じるかもしれませんが、Haskell で書くと

id' :: a -> a  -- あるいは forall a. a -> a
id' = \x -> x

と同じことだと思って良いでしょう。

:= の後の "fun A x => x" は「型 A と、型が A である値 x を受け取って、x を返す関数」を表します。では再び緑矢印で読み込ませてみましょう。これで無事 id を定義できました。

次に Command Pane を使って id に何か引数を渡して結果を見てみましょう。Command Pane 内の右側のテキストボックスに

id nat 5

と打ってください。Haskell の id や OCaml の identity では引数が一つで値だけを渡せばよいのですが、ここでは nat と 5 のように値の他にその値の型も渡さなければいけないことに注意してください。左側のテキストボックスは "Eval compute in" のままにして Ok ボタンを選択します。

Result for command Eval compute in id nat 5 .:
  = 5
  :nat

と表示されましたか。plus のときと同じく、"= 5" の 5 が id に nat と 5 を適用した結果です。

これで Coq で簡単な関数が定義できるようになりました。

証明 <=> プログラム

簡単な関数が書けるようになりましたが、Coq で証明をどんな風にするのか、そもそもプログラムの証明とは一体何がどうなっているのか、まだ全く分からないと思います。しかし実は、今の状態で読者の皆さんはあるプログラムに対する簡単な性質なら証明できる位置にいるのです。

プログラムの性質が証明できるとなると、簡単なプログラムを定義し、そのプログラムに対する簡単な性質を証明したくなるでしょう。ここでは、まず簡単なプログラムはすでに定義されていることにします。そして、その仮想的なプログラムに対する簡単な性質を証明してみましょう。

プログラムの性質とは、命題で表現するのですが、その命題を証明するとは、プログラムを定義することに他ならないのです。

もっと詳しく言うと、数理論理学における命題はプログラミングにおける型と一対一対応があり、証明はプログラムと一対一対応があります。それがどういうことかというと、命題は型を使って表現でき、ある命題が正しいことを証明するということは、その命題に対応する型をみたすプログラムを書くことに等しくなるのです。

簡単に書くと次のようになります。

命題	<->	型
証明	<->	プログラム

さっぱり分かりませんね。でも、諦めずに最後まで読んで下さい。

「え、命題って何?」という方のために簡単に説明すると、命題とは正しかったり間違っていたりする文の内容を指します(厳密に言うと違うという声も聞こえてきそうですが)。たとえば「このリンゴは赤い」や「全ての自然数 n に対して 2n = n + n」などのことで、これらは内容が正しいか間違っているか判定できますね。命題は間違った内容であってもいいので、「3 × 5 = 10」もまた命題です。逆に、「仕事しなさい」や「3 - 2」などは命題ではありません。

証明ができる、となると何らかのプログラムの性質などを示したいところですが、今の知識だけだとそれは難しいので、簡単のためまずは論理学のごく基本的な命題が成り立っていることを証明することにします。

はじめての証明

今、ある関数が仮想的に定義されており、その性質を表す命題を証明しようとしているのでした。そこで、こんな命題を考えます。

命題0. 任意の命題 A に対して「A ならば A」。

A に適当な命題を入れてみましょう。A を「1 - 1 = 0」とすると命題0は「1 - 1 = 0 ならば 1 - 1 = 0」となります。当たり前のことを言っていますね。命題0において A は任意の命題なので、A が正しい命題でも間違った命題でも命題0は正しい命題になります。

二階論理では命題0は記号を用いて次のように表現します。

∀A, A ⇒ A

∀は「任意の〜」の意味で、⇒は「ならば」の意味になります。記号を使うと簡潔かつ厳密に書くことができますが、直感的に分かりづらいというのであれば日本語で書かれた命題を見て意味を確認してください。

先程「命題は型と一対一対応がある」と書きましたが、この命題も型で表現でき、以下のようになります。

forall (A : Prop), A -> A

Prop とは Coq で「命題を表す型」の型であり、Prop は Type に含まれています。それはさておき、この型は見覚えがありますね。そう、id の型は

forall (A : Type), A -> A

であり、Type が Prop に変わっただけです。

実は、この id の型が命題0に対応しているのです。それではなぜこの型が命題0に対応しているのでしょうか。命題0を記号で表した形と対比させると、forall を ∀、-> を ⇒に置き換えればほとんど同じ形になるのが分かりますね。

この型の意味を考えてみましょう。"forall (A : Prop), A -> A" は id のときと同じように「型が Prop である任意の型 A に対して A -> A」という意味になります。Prop は命題の型でしたので、言いかえると「任意の命題 A に対して A -> A」となり、元の命題に近くなってきました。

ここで、"A -> B" という型は「A ならば B」という命題に対応している、ということが知られています。「型が "A -> B" のプログラム」は、「型 A のプログラム/値」を受けとると「型 B のプログラム/値」になりますね。一方「『A ならば B』の証明」は「命題 A の証明」を受け取って「命題 B の証明」をすればよいです。この二つを比べれば "A -> B" と「A ならば B」が対応していることが分かるでしょう。

これで元の命題に一致しましたね。大雑把な説明をしましたが、詳しくすると難しい内容になってしまうので、ここではこのような理解で納得してください。

「命題と型」の関係の例を挙げましたが、では「証明とプログラム」との関係はどうでしょう。命題 A の証明は型 A を持つプログラムに対応していることが知られています。つまり命題0を証明したい場合は "forall (A : Prop), A -> A" の型を持つプログラムを書けばよいのです。これなら今までの知識でできますね。早速命題0を証明してみましょう。

Definition prop0 : forall (A : Prop), A -> A :=
  fun A x => x.

もしこの定義に誤りがなく、CoqIDE が読み込んでくれれば証明は終了です。それでは CoqIDE に読み込ませてみましょう。背景が緑色に変わり、右下の枠に

prop0 is defined

と表示されましたか? もしそうなったら見事、命題0の証明ができたのです。はじめての証明は、これで完了です。ぱちぱち。

この「命題と型」、「証明とプログラム」間の関係をカリー・ハワード同型対応(Curry-Howard Isomorphism)と呼びます。どうしても納得のいかない方は調べてみてください。

二つ目の証明

それでは他の命題を考えてみましょう。

命題1. 任意の命題 A B C に対して、「B ならば C」ならば「A ならば B」ならば 「A ならば C」。

「ならば」や鉤括弧が沢山出てきてややこしいですね。では A、B、C をそれぞれ「これはネコ」「これは動物」「これは生物」として元の命題を考えると、「これが動物ならばこれは生物」ならば「これがネコならばこれは動物」ならば「これがネコならばこれは生物」となります。こう書くと少し理解しやすくなったでしょうか。ほかにも自分で例を考えてみましょう。

命題1も記号を使って表してみると、次のようになります。

∀A B C, (B ⇒ C) ⇒ (A ⇒ B) ⇒ (A ⇒ C)

早速これに対応する型を考えてみましょう。id のときと同じように、「任意の」や ∀ は forall、「ならば」や ⇒ は -> に置き換えていくと

forall (A B C : Prop), (B -> C) -> (A -> B) -> (A -> C)

となります。Coq で -> は右結合なので、最後の括弧は外して "(B -> C) -> (A -> B) -> A -> C" とも書けます。この型にも既視感がある方は多いのではないでしょうか。これは二つの関数を合成する関数ですね。Haskell だと (.) が同じ型を持ちます。

なぜこのように証明とプログラムが対応しているのかというと、数学で証明をしていくルールと型の推論規則が一致するから、という理解をしておいてください。

命題1も同じように証明をしてみましょう。型が "forall (A B C : Prop), (B -> C) -> (A -> B) -> (A -> C)" となる関数を書けば良いので、

Definition prop1 : forall (A B C : Prop), (B -> C) -> (A -> B) -> (A -> C) :=
  fun A B C f g x => f (g x).

となります。CoqIDE に読み込ませて "prop1 is defined" と表示されれば証明ができました。

プログラムの性質の証明

ここで気をつけてもらいたいのが、prop0 (id) や prop1 (.) は証明としてもプログラムとして使う関数としても意味がありましたが、Coq でほとんどの関数は「証明の意味で使う関数」と「プログラムに使う関数」に分かれています。

たとえば、二つのリストを結合する関数 app が定義されているとします。リスト l と l' の結合を app l l' と表記します(具体的なリストや app の扱い方は3章で紹介します)。では、リストの結合に関するこんな性質を証明したいとしましょう。

命題2. 任意の三つのリスト l1 l2 l3 に対して、 app l1 l3 = app l2 l3 ならば l1 = l2

これを型で表すと、

forall (A : Type)(l1 l2 l3 : list A), app l1 l3 = app l2 l3 -> l1 = l2

となります。型の中に、関数 app が現れてびっくりしたかもしれませんが、Coq ではこのような表現ができるようになっています。

Coq での "=" は厳密に言うと違いますが 数学の "=" に近いと思ってください。Haskell や OCaml で定義に使う "=" とは違います。これまでの説明から分かるように、この型をみたす関数を作ればこの命題が成り立つことが証明されます。実際に作れたとしてその関数を prop2 とすると

Definition prop2 : forall (A : Type)(l1 l2 l3 : list A), app l1 l3 = app l2 l3 -> l1 = l2
  := (* ここに定義が入る *).

と書けますね。ここで、prop2 は関数ですが、実際にプログラムに使える関数ではありません。あくまで prop2 は命題2が正しいことの保証になっている関数(証明)です。逆に、app はプログラムに使っている関数ではありますが、これ自体が何かの証明になっているとは言い難いです。

このように、Coq で何かプログラムに使いたい関数の性質を示したいときは、まずその関数を定義してから示したい性質を型で表し、その証明(型をみたす関数)を与える、という流れになります。

練習問題

話を戻して、今度は証明の練習をしてみましょう。それでは二問、証明問題を出すので読者の皆さん自身で証明してみてください。

問0. 任意の命題 A B に対して、A ならば 「A ならば B」ならば Bが成り立つ。
問1. 任意の命題 A B C に対して、「A ならば B ならば C」ならば「B ならば A ならば C」が成り立つ。

ここで、「ならば」は -> と同じく右結合だということに注意してください。「ならば」が沢山あってこの命題の意味はよく分からなくても、パズル感覚でこれまでのように型に直してみましょう。型が書ければ、あとはその型をみたす関数を書くだけです。もしかするとまたどこかで見覚えのある型かもしれません。

これまでは単純な命題でしたが、もっと複雑になるとどうでしょう。たとえば、こんな例を挙げてみます。

forall (P Q : Prop), (forall P : Prop, ((P -> Q) -> Q)) -> ((P -> Q) -> P) ->  P

これをみたすプログラムはちょっと考えたくないですね。できないことはないですが、面倒です。Coq では、このように面倒な命題を証明するために proof-editing mode というモードを使って楽に証明ができます。実は、Coq で証明といったらほとんどは proof-editing mode を使って証明するのですが、1章では証明とプログラムの対応を実感してもらうために関数定義の形での証明を紹介しました。proof-editing mode での証明のしかたは次回から解説します。

証明と聞くと難しそうですが、プログラムを書くだけだというなら身近に感じられた方も多いのでは? それではまた次回お会いしましょう。